Given a bipartite graph: “n” vertices on the left, “m” on the right and edges. The question is: how many edges in this graph are crossed?

In this example n=5, m=4, ten edges: 1-1, 1-2, 2-1, 2-2, 3-3, 4-1, 4-3, 5-1, 5-2, 5-4, a number of crossings: 10.

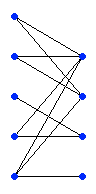
Crossings are always considered in pairs. For example, if three edges are crossed in one physical point, formally there are still three crossings, not one.

O(n*m) solution exists.